

Hence, surface area (A) of the octahedron=2×√3×a² Seeing that the area of an equilateral triangle is =√3/4×side²Īrea of one side of the octahedron = Area of an equilateral triangle Suppose that the length of each side of the octahedron be 'a' How to Find the Area of a Regular Octahedron?Ī regular octahedron is composed of 8 equilateral sides. This shape consists of the symmetry of C3v and is one of the three common shapes for pentacoordinate transition metal complexes, in addition to the pentagonal bipyramid and the capped trigonal prism.Įxamples of the capped octahedral molecular geometry include the heptafluoromolybdate (MoF−7) and the heptafluorotungstate (WF−7) ions. In chemistry, the capped octahedron is a part of molecular geometry that depicts the shape of compounds where 7 atoms or groups of atoms or ligands are organized around a central atom describing the vertices of a gyroelongated triangular pyramid. The angle between octahedron edges is 60 degrees while a dihedral angle measures 109.28 degrees. The formula to calculate the octahedron’s volume surface area is 2×√3×a².
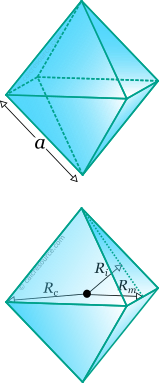
The formula to calculate the octahedron’s volume is 2/√3×a².
Octahedron sides by faces are 8 faces and 12 edges. The word is commonly used to refer to the regular octahedron, a Platonic solid made up of 8 equilateral triangles, 4 of which meet at each vertex.įollowing are the properties of a regular octahedron:Īn octahedron consists of 6 vertices and each vertex meets the 4 edges. It is one of the five octahedron platonic solid having equilateral triangular faces. The term octahedron is derived from the Greek terminology "oktaedron" which indicates "8 faced." That being said, an octahedron is a polyhedron having 8 faces, 12 edges, and 6 vertices.


 0 kommentar(er)
0 kommentar(er)
